문제 링크
https://www.acmicpc.net/problem/11660
[Silver I] 구간 합 구하기 5 - 11660
메모리: 129056 KB, 시간: 1268 ms
다이나믹 프로그래밍, 누적 합
2024년 9월 2일 10:38:04
N×N개의 수가 N×N 크기의 표에 채워져 있다. (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오. (x, y)는 x행 y열을 의미한다.
예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.

여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3+4+5+4+5+6 = 27이고, (4, 4)부터 (4, 4)까지 합을 구하면 7이다.
표에 채워져 있는 수와 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네 개의 정수 x1, y1, x2, y2 가 주어지며, (x1, y1)부터 (x2, y2)의 합을 구해 출력해야 한다. 표에 채워져 있는 수는 1,000보다 작거나 같은 자연수이다. (x1 ≤ x2, y1 ≤ y2)
총 M줄에 걸쳐 (x1, y1)부터 (x2, y2)까지 합을 구해 출력한다.
기존 구간합 구하기의 심화 버전 문제이다.
구간합 구하기 풀이 링크
https://9401ndk.tistory.com/90
백준 - 구간 합 구하기 4 (11659)
문제 링크https://www.acmicpc.net/problem/11659[Silver III] 구간 합 구하기 4 - 11659성능 요약메모리: 55544 KB, 시간: 548 ms분류누적 합제출 일자2024년 8월 22일 13:19:58문제 설명수 N개가 주어졌을 때, i번째 수부
9401ndk.tistory.com
1차원이 아닌, 2차원 배열의 구간합을 구하는 문제이다.
이전 문제와 동일하게 연산 횟수가 많으므로, 시간 복잡도에 신경써서 풀어나가야한다.
2차원 합배열을 구하는 공식은 다음과 같다.
2차원 합배열 초기화 공식
D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]

합배열 요소를 연산하기 위해 이전 인덱스 요소의 값이 필요하기 때문에, 원본 배열과 합배열을 초기화할 때 길이를 +1하여 선언하였다.
2차원 배열이기 때문에, 2중 for문으로 1행씩 연산을 진행한다.


i=1, j=1 로 가정할 때 각 요소를 연산하는 과정이다. 원본 배열값에 해당하는 A[i][j] 에 이전 인덱스의 값들을 합산한다.
결과적으로 i=1 에 해당하는 1행의 연산이 완료되었을 때, 결과는 다음과 같다.

행의 끝까지 합배열 초기화를 진행한 결과이다.
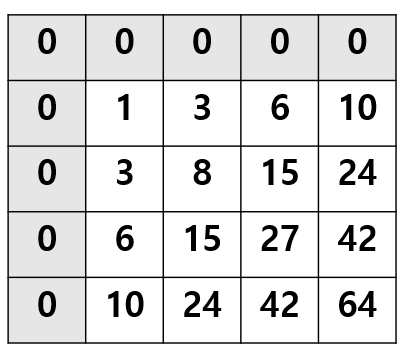
해당 합배열에서 구하고자 하는 구간합의 범위를 (2, 2), (3, 4) 라고 가정한다. 해당 값의 범위는 표로 보았을 때 아래와 같다.

해당 범위의 값을 구하기 위해서 (3, 4)까지의 구간합에서 아래 범위의 구간합을 뺄셈할 것이다.

우리는 이미 특정 구간의 합에 해당하는 값을 계산한 합배열을 만들어 둔 상태이므로, 합배열의 특정 지점의 값만 더하거나 빼주면 된다.
단, 구간합을 뺄셈할 범위에 해당하는 (1, 4) / (4, 1) 지점의 구간합은 공통적으로 (1, 1)의 범위의 합을 포함하고 있으므로 2번 뺄셈되게 되므로, (1, 1)의 구간합을 한 번 더해주는 것이다.

따라서, 주어진 지점의 구간합으로 최종 구간합을 구하는 공식은 다음과 같다.
D[x2][y2] - D[x1-1][y2] - D[x2][y1-1] - D[x1-1][y1-1]
결과값은 42 - 10 - 6 + 1 = 27 이다.

답안
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int[][] orginArr = new int[N+1][N+1];
// 원본배열 생성
for(int i=1; i<=N; i++){
StringTokenizer originLine = new StringTokenizer(br.readLine());
for(int j=1; j<=N; j++){
orginArr[i][j] = Integer.parseInt(originLine.nextToken());
}
}
// 합배열 생성
int[][] sumArr = new int[N+1][N+1];
for(int i=1; i<=N; i++){
for(int j=1; j<=N; j++){
sumArr[i][j] = orginArr[i][j] + sumArr[i-1][j] + sumArr[i][j-1] - sumArr[i-1][j-1];
}
}
int[] result = new int[M];
// 결과 출력
for(int i=0; i<M; i++){
StringTokenizer rangeLine = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(rangeLine.nextToken());
int y1 = Integer.parseInt(rangeLine.nextToken());
int x2 = Integer.parseInt(rangeLine.nextToken());
int y2 = Integer.parseInt(rangeLine.nextToken());
result[i] = sumArr[x2][y2] - sumArr[x2][y1-1] - sumArr[x1-1][y2] + sumArr[x1-1][y1-1];
}
for (int i : result){
System.out.println(i);
}
br.close();
}
}
후기
책에 나와있는 풀이 방법을 이해하며 풀어보려고 노력하는데, 수리적 사고가 부족해서인지 어렵게 느껴졌다.
그래프가 다차원으로 갈수록 머릿속에 그리는 것이 어렵기 때문에, 디버깅 모드로 값이 어떻게 변경되어지는지 확인하면서 진행하는게 더 수월했다. 각 공식의 의미가 잘 이해되지 않아서 직접 표로 그려보았는데 이해에 도움이 많이 되었다.
'코딩 테스트 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 - 구간 합 구하기 4 (11659) (1) | 2025.03.26 |
|---|---|
| 백준 - 문자열 10809 (0) | 2023.05.21 |
| 백준 - 1차원 배열 10810 (0) | 2023.05.12 |
| 백준 - 입출력과 사칙연산 2257 (0) | 2023.04.27 |



